Feature Engineering & Selection with R
One of the most important steps in any Data Science project, or rather the most important one, is data cleaning and transformation. It’s said that most of the time is spent in this particular step.
This step consists mainly of cleaning the messy data, getting it in shape for the model, transforming variables into more descriptive ones (Feature Engineering) and choosing the best variables for the predictive model we will use (Feature Selection).
Here we will use R to demonstrate some of the techniques used in these two major concepts: Feature Engineering and Selection.
We will use the custdata dataset from Practical Data Science with R book which I really recommend.
We will read the data into R and have a look at it.
The data can be downloaded from https://github.com/WinVector/zmPDSwR/blob/master/Custdata/custdata.tsv
Github Link: https://github.com/MNoorFawi/feature-engineering-and-selection-r
custdata <- read.table('custdata.tsv', header = TRUE, sep = '\t')
head(custdata)
## custid sex is.employed income marital.stat health.ins
## 1 2068 F NA 11300 Married TRUE
## 2 2073 F NA 0 Married TRUE
## 3 2848 M TRUE 4500 Never Married FALSE
## 4 5641 M TRUE 20000 Never Married FALSE
## 5 6369 F TRUE 12000 Never Married TRUE
## 6 8322 F TRUE 180000 Never Married TRUE
## housing.type recent.move num.vehicles age state.of.res
## 1 Homeowner free and clear FALSE 2 49 Michigan
## 2 Rented TRUE 3 40 Florida
## 3 Rented TRUE 3 22 Georgia
## 4 Occupied with no rent FALSE 0 22 New Mexico
## 5 Rented TRUE 1 31 Florida
## 6 Homeowner with mortgage/loan FALSE 1 40 New York
summary(custdata)
## custid sex is.employed income
## Min. : 2068 F:440 Mode :logical Min. : -8700
## 1st Qu.: 345667 M:560 FALSE:73 1st Qu.: 14600
## Median : 693403 TRUE :599 Median : 35000
## Mean : 698500 NA's :328 Mean : 53505
## 3rd Qu.:1044606 3rd Qu.: 67000
## Max. :1414286 Max. :615000
##
## marital.stat health.ins
## Divorced/Separated:155 Mode :logical
## Married :516 FALSE:159
## Never Married :233 TRUE :841
## Widowed : 96
##
##
##
## housing.type recent.move num.vehicles
## Homeowner free and clear :157 Mode :logical Min. :0.000
## Homeowner with mortgage/loan:412 FALSE:820 1st Qu.:1.000
## Occupied with no rent : 11 TRUE :124 Median :2.000
## Rented :364 NA's :56 Mean :1.916
## NA's : 56 3rd Qu.:2.000
## Max. :6.000
## NA's :56
## age state.of.res
## Min. : 0.0 California :100
## 1st Qu.: 38.0 New York : 71
## Median : 50.0 Pennsylvania: 70
## Mean : 51.7 Texas : 56
## 3rd Qu.: 64.0 Michigan : 52
## Max. :146.7 Ohio : 51
## (Other) :600
dim(custdata)
## [1] 1000 11
NA Imputation
We will begin with imputing the missing values.
### sum of all missing fields in the data and looking at the columns containing them
sum(is.na(custdata))
## [1] 496
missing_cols <- table(which(is.na(custdata), arr.ind = T)[, 2])
summary(custdata[, as.numeric(names(missing_cols))])
## is.employed housing.type recent.move
## Mode :logical Homeowner free and clear :157 Mode :logical
## FALSE:73 Homeowner with mortgage/loan:412 FALSE:820
## TRUE :599 Occupied with no rent : 11 TRUE :124
## NA's :328 Rented :364 NA's :56
## NA's : 56
##
##
## num.vehicles
## Min. :0.000
## 1st Qu.:1.000
## Median :2.000
## Mean :1.916
## 3rd Qu.:2.000
## Max. :6.000
## NA's :56
First we will deal with the missing data from a categorical variable
As we see most of the missing data comes from one column “is.employed”. This can mean a lot, so this is one of the situations where domain knowledge comes into help to know what is exactly this data can represent.
One of the solutions is to transform missing values into a new category:
custdata$is.employed <- as.factor(
ifelse(is.na(custdata$is.employed),
"missing",
ifelse(custdata$is.employed == T,
"employed",
"not employed")
))
summary(custdata$is.employed)
## employed missing not employed
## 599 328 73
Dealing with missing values from a numeric variable
We will insert some NA values randomly into “income”” variable;
summary(custdata$income)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -8700 14600 35000 53505 67000 615000
custdata[sample(1:nrow(custdata), 56), "income"] <- NA
summary(custdata$income)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -8700 14400 34350 52643 65000 615000 56
The most common solution with NA values in a numeric value is to impute them into the mean or average value in the variable:
mean_income <- mean(custdata$income, na.rm = TRUE)
custdata$income <- ifelse(is.na(custdata$income),
mean_income,
custdata$income)
summary(custdata$income)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -8700 15000 36740 52643 62000 615000
The data is yes affected but not too much from the original one.
Dropping rows with missing values
if the missing values come mainly from some specific rows, we can confidently drop them. Here we can see that almost all the missing values for “recent.move” and “num.vehicles” are accompanied with the missing values for “housing.type” variable.
summary(custdata[is.na(custdata$housing.type),
c("recent.move", "num.vehicles")])
## recent.move num.vehicles
## Mode:logical Min. : NA
## NA's:56 1st Qu.: NA
## Median : NA
## Mean :NaN
## 3rd Qu.: NA
## Max. : NA
## NA's :56
So we will drop the rows containing them all.
custdata <- custdata[complete.cases(custdata),]
d <- custdata # we will use it later
dim(custdata)
## [1] 944 11
Variable Transformation
Log Transformation for numeric variables.
Some numeric variables have log distribution which can be spotted with a density plot it is skewed to one side:
suppressMessages(library(ggplot2))
suppressMessages(library(scales))
## log_income
ggplot(custdata, aes(x = income)) +
geom_density(fill = "purple", color = "white", alpha = 0.5) +
scale_x_continuous(labels = dollar) + theme_minimal()
When we take the log of the variable:
ggplot(custdata, aes(x = income)) +
geom_density(fill = "purple", color = "white", alpha = 0.5) +
scale_x_log10(breaks = c(100, 1000, 10000, 100000), labels = dollar) +
xlab("log income") + theme_minimal()
Binarization
Another way to deal with numeric variable is to binarize it or to transform it into a binary categorical variable if the the numeric variableis distributed around a specifici number or threshold.
ggplot(custdata, aes(x = income, fill = health.ins)) +
geom_density(color = 'white', alpha = 0.6, size = 0.5) +
theme_minimal() + scale_fill_brewer(palette = 'Set1') +
scale_x_log10(breaks = c(100, 1000, 10000, 100000), labels = dollar)
ggplot(custdata, aes(x = income, y = as.numeric(health.ins))) +
geom_point() + geom_smooth() + scale_x_log10(labels = dollar) +
theme_minimal()
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'
Here we can see that above 20K or 30k income, people tend to have “health insurance” more than people below this threshold.
binarized_income <- ifelse(custdata$income >= 30000,
">=30K",
"<30K")
table(binarized_income)
## binarized_income
## <30K >=30K
## 370 574
Descretization
One more way is to discretize numeric values into categorical ranges:
probs <- quantile(custdata$age, probs = seq(0.1, 1, 0.1), na.rm = T)
age_groups <-
cut(custdata$age,
breaks = probs, include.lowest = T)
summary(age_groups)
# to remove NAs
#gp_with_no_na <- addNA(age_groups)
#levels(gp_with_no_na) <- c(levels(age_groups), "newlevel")
#summary(gp_with_no_na)
## [29,36] (36,41] (41,46] (46,50] (50,55] (55,60] (60,67] (67,76]
## 115 99 92 87 101 86 102 87
## (76,147] NA's
## 92 83
Here, looking at the age variable, we are not interested very much with the values themselves. But the age ranges are rather more important.
Normalization
Another way to deal with numeric variables is to normalize them. There are two ways to normalize:
1- against the variable range (max and min)
range_normalize <- function(x){
(x - min(x)) / (max(x) - min(x))
}
custdata[, "range_normalized_age"] <- range_normalize(custdata$age)
summary(custdata$range_normalized_age)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.2659 0.3409 0.3541 0.4363 1.0000
2- against Mean/Average or Median of the variable itself
summary(custdata$age)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.00 39.00 50.00 51.93 64.00 146.68
custdata$normalized_age <- custdata$age / mean(custdata$age)
summary(custdata$normalized_age)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0000 0.7510 0.9628 1.0000 1.2324 2.8244
## more insights
custdata$age_gps <- factor(ifelse(custdata$normalized_age >= 1, "old", "young"))
ggplot(custdata, aes(x = age, fill = age_gps)) +
geom_density(color = "white", alpha = 0.5) + theme_minimal() +
scale_fill_brewer(palette = 'Set1')
3- against mean/average or median of a group or category
suppressMessages(library(dplyr))
table(custdata$state.of.res)
##
## Alabama Alaska Arizona Arkansas California
## 10 3 9 6 91
## Colorado Connecticut Delaware Florida Georgia
## 11 14 1 45 24
## Hawaii Idaho Illinois Indiana Iowa
## 4 3 49 28 10
## Kansas Kentucky Louisiana Maine Maryland
## 4 15 15 5 16
## Massachusetts Michigan Minnesota Mississippi Missouri
## 24 51 20 2 20
## Montana Nebraska Nevada New Hampshire New Jersey
## 2 8 4 5 36
## New Mexico New York North Carolina North Dakota Ohio
## 6 70 15 1 49
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 11 7 65 2 14
## South Dakota Tennessee Texas Utah Vermont
## 5 21 54 4 3
## Virginia Washington West Virginia Wisconsin Wyoming
## 26 17 12 26 1
median_income <- custdata %>% group_by(state.of.res) %>%
summarise(state_median_income = median(income, na.rm = TRUE))
dim(median_income)
## [1] 50 2
custdata <- merge(custdata, median_income,
by = "state.of.res")
custdata$normalized_income <- with(custdata, income / state_median_income)
summary(custdata$normalized_income)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## -0.1933 0.4600 1.0000 1.4147 1.6756 15.3750 1
Scaling
One more way is to scale the variables.
custdata$scaled_age <- (custdata$age - mean(custdata$age)) / sd(custdata$age)
summary(custdata$scaled_age)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -2.8166 -0.7014 -0.1048 0.0000 0.6545 5.1387
The idea behind normalizing and scaling is to get all the numeric variables into a reasonable range so that variables with bigger numbers like income don’t have greater effect in the model than those of smaller numbers like age
Dealing with Categorical Variables:
Sometimes we need to transform categorical variables for example when a variable contains many categories or using an algorithm that only accepts numbers.
One-hot encoding
One way is to one-hot encode the variable: transform each category into a new column containing 1 or 0 according to their existence.
### one-hot encoding
vars <- colnames(custdata)
## to one hot encode factor values and normalize numeric ones if needed
cat_vars <- vars[sapply(custdata[, vars], class) %in%
c("factor", "character", "logical")]
cat_vars <- cat_vars[-1] #state of res
custdata2 <- custdata[, cat_vars]
for (i in cat_vars) {
dict <- unique(custdata2[, i])
for (key in dict) {
custdata2[[paste0(i, "_", key)]] <- 1.0 * (custdata2[, i] == key)
}
}
# to remove the original categorical variables
#custdata[, which(colnames(custdata) %in% cat_vars)] <- NULL
head(custdata2)
## sex is.employed marital.stat health.ins
## 1 F missing Married TRUE
## 2 F employed Divorced/Separated TRUE
## 3 F employed Widowed TRUE
## 4 M not employed Married TRUE
## 5 F employed Married TRUE
## 6 M employed Married TRUE
## housing.type recent.move age_gps sex_F sex_M
## 1 Homeowner free and clear FALSE old 1 0
## 2 Rented FALSE young 1 0
## 3 Rented FALSE old 1 0
## 4 Homeowner with mortgage/loan FALSE old 0 1
## 5 Homeowner with mortgage/loan FALSE old 1 0
## 6 Rented FALSE young 0 1
## is.employed_missing is.employed_employed is.employed_not employed
## 1 1 0 0
## 2 0 1 0
## 3 0 1 0
## 4 0 0 1
## 5 0 1 0
## 6 0 1 0
## marital.stat_Married marital.stat_Divorced/Separated
## 1 1 0
## 2 0 1
## 3 0 0
## 4 1 0
## 5 1 0
## 6 1 0
## marital.stat_Widowed marital.stat_Never Married health.ins_TRUE
## 1 0 0 1
## 2 0 0 1
## 3 1 0 1
## 4 0 0 1
## 5 0 0 1
## 6 0 0 1
## health.ins_FALSE housing.type_Homeowner free and clear
## 1 0 1
## 2 0 0
## 3 0 0
## 4 0 0
## 5 0 0
## 6 0 0
## housing.type_Rented housing.type_Homeowner with mortgage/loan
## 1 0 0
## 2 1 0
## 3 1 0
## 4 0 1
## 5 0 1
## 6 1 0
## housing.type_Occupied with no rent recent.move_FALSE recent.move_TRUE
## 1 0 1 0
## 2 0 1 0
## 3 0 1 0
## 4 0 1 0
## 5 0 1 0
## 6 0 1 0
## age_gps_old age_gps_young
## 1 1 0
## 2 0 1
## 3 1 0
## 4 1 0
## 5 1 0
## 6 0 1
Conditional Probability
Another way is to convert every category into its odds ratio. This technique is useful when dealing with variables with so many categories. N.B. This technique assumes that historical data is available for computing the statistics.
table(custdata$marital.stat) #predictor
##
## Divorced/Separated Married Never Married
## 149 507 198
## Widowed
## 90
table(custdata$health.ins) #outcome
##
## FALSE TRUE
## 137 807
with(custdata, table(marital.stat, health.ins))
## health.ins
## marital.stat FALSE TRUE
## Divorced/Separated 20 129
## Married 58 449
## Never Married 54 144
## Widowed 5 85
odds_ratio <- function(x, y, pos, logarithm = FALSE) {
prob_table <- table(as.factor(y), x)
vals <- unique(y)
neg <- vals[which(vals != pos)]
outcome_prob <- sum(y == pos, na.rm = T) / length(y)
odds_ratio <-
(prob_table[pos,] + 0.001) / (prob_table[neg, ] + 0.001)
odds <- odds_ratio[x]
odds[is.na(odds)] <- outcome_prob
if (logarithm) {
odds <- log(odds)
}
odds
}
vars <- colnames(custdata)
custdata3 <- custdata
cat_vars <- vars[sapply(custdata[, vars], class) %in%
c("factor", "character", "logical")]
cat_vars <- cat_vars[which(cat_vars != "health.ins")]
custdata3[, cat_vars] <- apply(custdata3[, cat_vars], 2,
function(x, y, pos) {
odds_ratio(x, as.factor(custdata3$health.ins),
"TRUE")
})
head(custdata3)
## state.of.res custid sex is.employed income marital.stat health.ins
## 1 8.992008 799074 6.083249 9.370060 56500 7.741263 TRUE
## 2 8.992008 572341 6.083249 6.120420 16000 6.449728 TRUE
## 3 8.992008 1089530 6.083249 6.120420 48000 16.996801 TRUE
## 4 8.992008 988264 5.740198 1.703678 5000 7.741263 TRUE
## 5 8.992008 1197386 6.083249 6.120420 25000 7.741263 TRUE
## 6 8.992008 999444 5.740198 6.120420 24000 7.741263 TRUE
## housing.type recent.move num.vehicles age range_normalized_age
## 1 12.082410 6.321381 3 74 0.5044989
## 2 3.232532 6.321381 1 36 0.2454319
## 3 3.232532 6.321381 1 54 0.3681479
## 4 10.444182 6.321381 5 55 0.3749654
## 5 10.444182 6.321381 2 55 0.3749654
## 6 3.232532 6.321381 2 24 0.1636213
## normalized_age age_gps state_median_income normalized_income
## 1 1.4249110 12.575407 23000 2.4565217
## 2 0.6932000 3.769204 23000 0.6956522
## 3 1.0398000 12.575407 23000 2.0869565
## 4 1.0590555 12.575407 23000 0.2173913
## 5 1.0590555 12.575407 23000 1.0869565
## 6 0.4621333 3.769204 23000 1.0434783
## scaled_age
## 1 1.1968218
## 2 -0.8641455
## 3 0.1121022
## 4 0.1663382
## 5 0.1663382
## 6 -1.5149773
Feature Selection
There are so many techinques to select the best variables for our predictive models.
1- Filter methods: to filter variables based on some criteria like R-Squared.
2- Wrapper methods: This method treats the features selection process as a search problem, where different combinations of features are tested against performance criteria and compared with other combinations.
3- Embedded methods: like decision tree, the algorithm itself ranks the variables and select the best cutting criteria for them.
Here we are going to explore the Filtering Methods. We are going to modify the odds_ratio function to compute the conditional probability for both numeric and categorical variables building Single Variable Model for each variable and compute the loglikelihood for each one then compute the improvement of model deviance against null deviance for each single variable model and then compute the R-Squared for each single variable model and rank the variables according to their scores and then subset them based on a certain threshold.
## Single Variable Model Function
single_variable_model <- function(x, y, pos) {
if (class(x) %in% c("numeric", "integer")) {
# if numeric descretize it
probs <- unique(quantile(x, probs = seq(0.1, 1, 0.1), na.rm = T))
x <- cut(x, breaks = probs, include.lowest = T)
}
prob_table <- table(as.factor(y), x)
vals <- unique(y)
neg <- vals[which(vals != pos)]
outcome_prob <- sum(y == pos, na.rm = T) / length(y) #outcome probability
cond_prob <-
(prob_table[pos,] + 0.001 * outcome_prob) /
(colSums(prob_table) + 0.001) # probability of outcome given variable
cond_prob_model <- cond_prob[x]
cond_prob_model[is.na(cond_prob_model)] <- outcome_prob
cond_prob_model
}
Split data into train and test.
head(d) #original custdata
## custid sex is.employed income marital.stat health.ins
## 1 2068 F missing 11300 Married TRUE
## 2 2073 F missing 0 Married TRUE
## 3 2848 M employed 4500 Never Married FALSE
## 4 5641 M employed 20000 Never Married FALSE
## 5 6369 F employed 12000 Never Married TRUE
## 6 8322 F employed 180000 Never Married TRUE
## housing.type recent.move num.vehicles age state.of.res
## 1 Homeowner free and clear FALSE 2 49 Michigan
## 2 Rented TRUE 3 40 Florida
## 3 Rented TRUE 3 22 Georgia
## 4 Occupied with no rent FALSE 0 22 New Mexico
## 5 Rented TRUE 1 31 Florida
## 6 Homeowner with mortgage/loan FALSE 1 40 New York
set.seed(13)
d$split <- runif(nrow(d))
train <- subset(d, split <= 0.9)
test <- subset(d, split > 0.9)
train$split <- test$split <- NULL
Function to calculate AUC for each Single Variable Model.
suppressMessages(library(ROCR))
auc <- function(model, outcome, pos) {
per <- performance(prediction(model, outcome == pos),
"auc")
as.numeric(per@y.values)
}
Build the Single Variable Model for each variable.
vars <- setdiff(colnames(train), c("custid", "health.ins"))
train[, paste0("svm_", vars)] <- apply(train[, vars], 2,
function(x, y, pos) {
single_variable_model(x, as.factor(train$health.ins),
"TRUE")
})
test[, paste0("svm_", vars)] <- apply(test[, vars], 2,
function(x, y, pos) {
single_variable_model(x, as.factor(test$health.ins),
"TRUE")
})
head(train)
## custid sex is.employed income marital.stat health.ins
## 1 2068 F missing 11300 Married TRUE
## 2 2073 F missing 0 Married TRUE
## 3 2848 M employed 4500 Never Married FALSE
## 4 5641 M employed 20000 Never Married FALSE
## 6 8322 F employed 180000 Never Married TRUE
## 7 8521 M employed 120000 Never Married TRUE
## housing.type recent.move num.vehicles age state.of.res
## 1 Homeowner free and clear FALSE 2 49 Michigan
## 2 Rented TRUE 3 40 Florida
## 3 Rented TRUE 3 22 Georgia
## 4 Occupied with no rent FALSE 0 22 New Mexico
## 6 Homeowner with mortgage/loan FALSE 1 40 New York
## 7 Homeowner free and clear TRUE 1 39 Idaho
## svm_sex svm_is.employed svm_income svm_marital.stat svm_housing.type
## 1 0.8544974 0.8991934 0.9998589785 0.8888888 0.9379305
## 2 0.8544974 0.8991934 0.6136419363 0.8888888 0.7554862
## 3 0.8623656 0.8646616 0.0008579795 0.7294125 0.7554862
## 4 0.8623656 0.8646616 0.8000117651 0.7294125 0.7000159
## 6 0.8544974 0.8646616 0.9999647182 0.7294125 0.9214090
## 7 0.8623656 0.8646616 0.9999798368 0.7294125 0.9379305
## svm_recent.move svm_num.vehicles svm_age svm_state.of.res
## 1 0.8686730 0.8513932 0.8888872 0.8510640
## 2 0.7946434 0.9112899 0.8260884 0.9499977
## 3 0.7946434 0.9112899 0.6000518 0.8095262
## 4 0.8686730 0.8163274 0.6000518 0.8333376
## 6 0.8686730 0.8513011 0.8260884 0.8000009
## 7 0.7946434 0.8513011 0.9473638 0.9999530
head(test)
## custid sex is.employed income marital.stat health.ins
## 5 6369 F employed 12000 Never Married TRUE
## 34 46099 M employed 36880 Never Married TRUE
## 44 52436 F employed 139000 Married TRUE
## 47 53759 F missing 0 Married TRUE
## 55 67776 M employed 52000 Married TRUE
## 79 98086 M missing 52100 Married TRUE
## housing.type recent.move num.vehicles age state.of.res
## 5 Rented TRUE 1 31 Florida
## 34 Homeowner with mortgage/loan FALSE 2 65 Massachusetts
## 44 Homeowner with mortgage/loan FALSE 2 46 Pennsylvania
## 47 Homeowner with mortgage/loan FALSE 2 34 Ohio
## 55 Homeowner with mortgage/loan FALSE 1 38 Florida
## 79 Homeowner with mortgage/loan TRUE 2 69 Florida
## svm_sex svm_is.employed svm_income svm_marital.stat svm_housing.type
## 5 0.8936155 0.8135595 0.5001608 0.7142896 0.8222222
## 34 0.7592604 0.8135595 0.9998220 0.7142896 0.8372089
## 44 0.8936155 0.8135595 0.9998220 0.8541660 0.8372089
## 47 0.8936155 0.9374964 0.4286276 0.8541660 0.8372089
## 55 0.7592604 0.8135595 0.9999109 0.8541660 0.8372089
## 79 0.7592604 0.9374964 0.9998220 0.8541660 0.8372089
## svm_recent.move svm_num.vehicles svm_age svm_state.of.res
## 5 0.8333324 0.7812513 0.9999109 0.9999644
## 34 0.8202247 0.8974340 0.9999109 0.9999555
## 44 0.8202247 0.8974340 0.9999109 0.8999922
## 47 0.8202247 0.8974340 0.9999109 0.8000044
## 55 0.8202247 0.7812513 0.9999406 0.9999644
## 79 0.8333324 0.8974340 0.9999109 0.9999644
AUC for each built SVM
svm_vars <- grep("svm_", colnames(train), value = TRUE)
for(i in svm_vars){
train_svm_auc <- auc(train[, i], train$health.ins, "TRUE")
print(sprintf("%s: train_AUC: %4.3f",
i, train_svm_auc))
}
## [1] "svm_sex: train_AUC: 0.508"
## [1] "svm_is.employed: train_AUC: 0.591"
## [1] "svm_income: train_AUC: 0.941"
## [1] "svm_marital.stat: train_AUC: 0.633"
## [1] "svm_housing.type: train_AUC: 0.675"
## [1] "svm_recent.move: train_AUC: 0.535"
## [1] "svm_num.vehicles: train_AUC: 0.551"
## [1] "svm_age: train_AUC: 0.787"
## [1] "svm_state.of.res: train_AUC: 0.675"
Compute loglikelihood, deviance and R-Squared for the models and rank the variables.
loglikelihood <- function(y, py) {
sum(y * log(py) + (1 - y) * log(1 - py))
}
outcome <- "health.ins"
pos <- "TRUE"
pnull <- sum(train[, outcome] == pos) / length(train[, outcome])
null_deviance <- -2 * loglikelihood(as.numeric(train$health.ins), pnull)
sv_model_deviance <- c()
variable <- c()
for(i in svm_vars){
sv_model_deviance <- c(sv_model_deviance,
-2 * loglikelihood(as.numeric(train$health.ins),
train[, i]))
variable <- c(variable, i)
}
names(sv_model_deviance) <- variable
sv_model_deviance
## svm_sex svm_is.employed svm_income svm_marital.stat
## 686.2106 665.4148 313.3968 656.4158
## svm_housing.type svm_recent.move svm_num.vehicles svm_age
## 637.7329 682.3076 679.7469 562.8025
## svm_state.of.res
## 633.3886
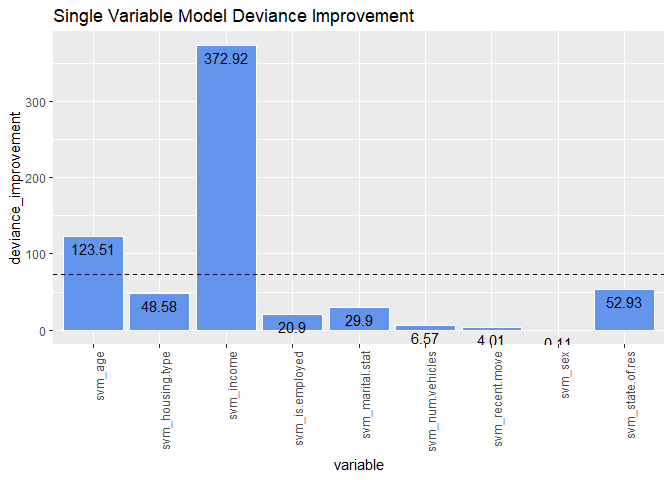
deviance_improvement <- null_deviance - sv_model_deviance
sort(deviance_improvement, decreasing = TRUE)
## svm_income svm_age svm_state.of.res svm_housing.type
## 372.9201848 123.5144166 52.9283802 48.5840938
## svm_marital.stat svm_is.employed svm_num.vehicles svm_recent.move
## 29.9011729 20.9021276 6.5700154 4.0093474
## svm_sex
## 0.1063151
ggplot(
data.frame(
variable = names(deviance_improvement),
deviance_improvement = round(deviance_improvement, 2)
),
aes(x = variable, y = deviance_improvement)
) +
geom_bar(stat = "identity", color = "white", fill = "cornflowerblue") +
# threshold
geom_hline(yintercept = mean(deviance_improvement), linetype = "dashed") +
geom_text(aes(label = deviance_improvement), color = "black", vjust = 1.5) +
theme(axis.text.x = element_text(angle = 90, hjust = 1)) +
ggtitle("Single Variable Model Deviance Improvement")
sv_pseudo_rsquared <- 1 - (sv_model_deviance / null_deviance)
sort(sv_pseudo_rsquared, decreasing = TRUE)
## svm_income svm_age svm_state.of.res svm_housing.type
## 0.5433643704 0.1799670170 0.0771194404 0.0707895860
## svm_marital.stat svm_is.employed svm_num.vehicles svm_recent.move
## 0.0435675854 0.0304555019 0.0095728588 0.0058418306
## svm_sex
## 0.0001549067
rsq <- data.frame(variable = names(sv_pseudo_rsquared),
Rsquared = round(sv_pseudo_rsquared, 2),
selected = ifelse(sv_pseudo_rsquared >= mean(sv_pseudo_rsquared),
"good candidate", "bad candidate"))
ggplot(rsq, aes(x = Rsquared, y = reorder(variable, Rsquared))) +
geom_point(aes(color = selected), size = 2) +
scale_color_brewer(palette = "Set1") +
theme_bw() +
theme(
# No vertical grid lines
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank(),
# horizontal grid
panel.grid.major.y = element_line(colour = "grey60", linetype = "dashed"),
legend.position = c(1, 0.55),
# Put legend inside plot area
legend.justification = c(1, 0.5)
) +
# threshold
geom_vline(xintercept = mean(sv_pseudo_rsquared), linetype = "dashed") +
xlab("SVM Pseudo R-Squared") + ylab("Variable") +
ggtitle("Single Variable Model Pseudo R-Squared")
Select Variables based on a threshold
selected_vars <- names(sv_pseudo_rsquared)[which(sv_pseudo_rsquared >= 0.1)]
selected_vars
## [1] "svm_income" "svm_age"
Build our classification model using the selected variables and evaluate it on test dataset calculating its train and test AUCs.
glm_model <- glm(health.ins ~ .,
data = train[, c("health.ins", selected_vars)],
family = binomial(link = "logit"))
summary(glm_model)
##
## Call:
## glm(formula = health.ins ~ ., family = binomial(link = "logit"),
## data = train[, c("health.ins", selected_vars)])
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.84741 0.09736 0.15017 0.26031 2.39533
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -10.9740 1.1975 -9.164 < 2e-16 ***
## svm_income 8.9233 0.8265 10.796 < 2e-16 ***
## svm_age 7.4017 1.1657 6.350 2.16e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 686.32 on 842 degrees of freedom
## Residual deviance: 302.25 on 840 degrees of freedom
## AIC: 308.25
##
## Number of Fisher Scoring iterations: 7
train$glm_model <- predict(glm_model, train,
type = "response")
auc(train$glm_model, train$health.ins, "TRUE")
## [1] 0.9540891
suppressMessages(library(WVPlots))
WVPlots::ROCPlot(train,
"glm_model", outcome, pos,
'train performance')
### On test dataset
test$glm_model <- predict(glm_model, test,
type = "response")
auc(test$glm_model, test$health.ins, "TRUE")
## [1] 0.9983266
WVPlots::ROCPlot(test,
"glm_model", outcome, pos,
'test performance')









Leave a Reply